Conic

Conic can be represented by 6 parameters, $$ax^2 + bxy + cy^2 + dx + ey + f = 0$$

 

it can also represented with matrix form like this:

\begin{pmatrix}
a &b/2  &d/2 \\ 
b/2 &c  &e/2 \\ 
d/2 &e/2  &f 
\end{pmatrix}

 

The relationship between point and conic is like this:

 

$$x^TCx=0 \ \ \ where \ x = (x_1, x_2, 1)$$

 

Dual conic C*: composed of a bunch of lines which is a tangent line.

 

$$C^* = kC^{-1}$$ 

** Characteristics of conic

 

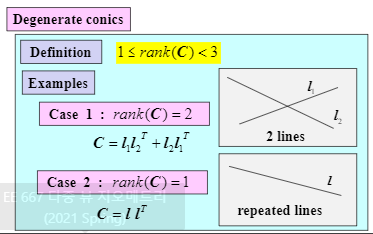
- Degenerate conic:  a rank of the matrix C is lower than 3

 

(Point) Conic: it can be represented by the line.

two lines(rank: 2), one line(rank: 1)

Degenerated (point) conic

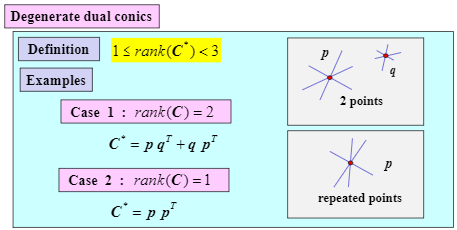
Dual conic: can be represented by the point.

two points(rank: 2), one point(rank: 1)

 

Degenerated dual conic