Affine reconstruction에서 가장 중요한 것은 plane at infinity이다.
Metric retification에서는 CDCP, metric reconstruction은 IAC를 알면 된다.
양 이미지에 대해 point correspondence를 찾고, 이 조건을 이용해 F를 구한다.
이후 F로 부터 P, P'을 아무거나 찾을 수 있다. 이로 부터 가상의 3차원 좌표를 구할 수 있다.
본 구조물 (3D)에 대해 평행성을 만들어 주기위해, 3D Homography => affine recon
닮은꼴 변환 3D Homography => Metirc recon
(P와 P'을 이용하여 어떻게 3D recon을 하는지?? => triangulation+ F를 어떻게 구하는지? => 두 이미지간의 correspondence 관계 식으로)
P'의 General 한 표현으로 finite camera로 만들 수 있다. =>중요하다고 강조하심
Triangulation
Direction vector: Plane at infinity와 만나는 vector d = M^-1 x 와 d'을 구하여 교점을 구할 수 있다.(***********)

d와 d'이 구해지면 두개의 교점을 구하면 3차원 좌표를 얻을 수 있다.
Affine recon: vanishing point에 대한 correspondence를 찾고 recon을 했을 때, 복원 된 3D 좌표( Image of infinity plane)을 무한대로 보낸다.
두영상에 대해 vanishing point 3쌍을 찾는다. 3D recon이 된 3개의 point로 구성되는 평면을 구한다.
그 평면을 plane at infinity로 보내는 homography (H)를 구한다.
구한 H를 PH, P'H 해주고 3D recon하면 affine 성질이 보존된다.
Infinity homography : plane at infinity 상에 있는 point( vanishing point)를 두 카메라로 찍었을 때, image plane이 homography
F를 알면 e, e'의 쌍을 알 수 있기 때문에, 3개의 vanishing point 쌍을 구하면 infinite H를 구할 수 있다.
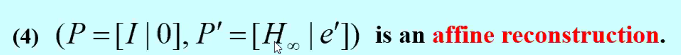
Metric Recon: IAC를 가지고 가꼬논다.
Metric Recon을 하는 Homography는 affine transformation이어야 하므로 A를 구하는 것이 목표이다.
